- Home
- Research
- Fiber Research and Technology
- Research results
- Dispersion Analysis in a Tunable Fiber Laser
Dispersion Analysis in a Tunable Fiber Laser
28.03.2019
The dispersion properties of fibers describe the wavelength dependence of light propagation in waveguides. This is particularly interesting for optimizing the propagation properties of ultrashort laser pulses along the fiber. At Leibniz IPHT, a laser-integrated measuring concept has been developed for the dispersion properties of fibers based on a special resonator structure of a tunable laser.
By T. Tiess // A. Hartung // M. Becker // C. Chojetzki // M. Rothhardt // H. Bartelt // M. Jäger
Tunable lasers are characterized by a tunable emission wavelength (λL), which can be adapted within the amplification range of the laser-active medium, as required by different applications . This is crucially important for spectrally demanding applications such as in telecommunications, in material processing, and especially in biophotonics. Fiber lasers not only offer high efficiency and excellent beam quality for these applications, but they are also characterized by a very robust, compact, and low-maintenance design, especially in the fiber-integrated layout. In addition, there are typically very wide amplification ranges of active fibers, which enable a large working window for λL.
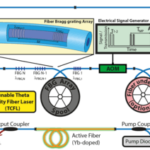
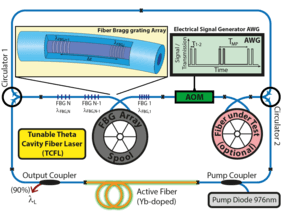
This paper addresses a new field of application for tunable lasers by measuring the dispersion properties of fiber optic components. This method is based on a tuning concept developed at Leibniz IPHT based on a theta cavity fiber laser (TCFL) (see Fig. 1), which uses a discrete fiber Bragg grating (FBG) array as a spectral filter to adjust λL. This fiber-integrated filter allows custom tuning ranges over large spectral bandwidths. Spectral tuning is based on a timing control mechanism. Using optical gating (switching short transmission windows), the pulse propagation time in the resonator is controlled; thus, the emission wavelength of the laser is coupled to a specific response line of the filter and both the pulse duration (in the low nanosecond range) and the repetition rate are electrically adjusted. The theta layout of the fiber laser matches the resonator lengths for all emission wavelengths so that the repetition rate is constant across the entire tuning range. However, the dispersion properties of the resonator components lead to minimal wavelength-dependent variations of the exact pulse round trip time (TMP,0). These form the basis for measuring dispersion properties across the tuning range of the laser.
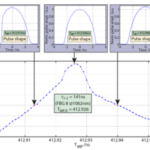
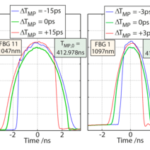
Fig. 2 depicts two graphs showing the pulse shape of the laser signal for slightly different repetition rates (equivalent to the modulation period (TMP)) for two different emission wavelengths. The measurements of the green lines are carried out at the exact pulse propagation time in the resonator and show a high symmetry. The red and blue measurements are taken with a slightly out-of-tune modulation period (TMP) and show an asymmetrical steepening of one pulse side each. In this mode, the laser works with a repetition rate that is slightly detuned with the precise pulse propagation time (TMP,0) at the respective wavelength. Notably, the sensitivity of this effect is in the low picosecond range of TMP(despite measuring electronics with a resolution in the range of 1 ns). A comparison of the two graphs shows that the precise pulse propagation time (TMP,0) varies by 156 ps due to wavelength detuning.
This effect provides the basis for the analysis of dispersion properties. It enables the precise measurement of the pulse propagation time in the resonator as a function of the emission wavelength of the laser. The correlation with the group velocity of the pulses allows the effective dispersion parameter (Dλ) of the total resonator to be investigated within the tuning range. The analysis of individual fiber components, such as a fiber under test (FUT), is based on comparative measurements in the resonator with and without a sample (see Fig. 1).
For this concept, the changes in the pulse shape were quantified as a function of TMPand λLusing a convolution analysis. An exemplary measurement of this self-convolution function for one wavelength is shown in Fig. 3. The function reaches its maximum with a symmetrical pulse shape, so that TMP,0is determined from the peak of this curve for the corresponding wavelength. This provides an automated procedure for measuring the pulse propagation time as a function of the wavelength, both in the reference resonator and in the setup with an FUT. The result for the test fiber is the dispersion parameter Dλ.
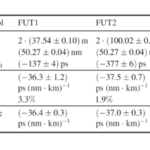
This scenario was applied to two FUT segments (FUT1 and FUT2). Both describe the same fiber type (Nufern PM980-XP) but with slightly different specifications from different batches. The measurement results for dispersion analysis across the full tuning range of 50 nm are shown in the table in Fig. 4. While Dλ,exp.was measured with FUT1, FUT2 shows a reproducible deviation. As a reference, both samples were also examined with a conventional, free-space-coupled interferometric approach. The corresponding values for Dλ,exp.2in the table in Figure 4 show very good agreement and verify the measurement with the TCFL. The investigations have shown that the segments FUT1 and FUT2 of the same fiber type exhibit production-related deviations, which result in slight differences in dispersion.
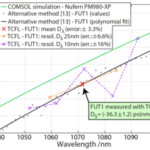
If one evaluates the measurement of the pulse propagation time in the TCFL across incremental ranges of the tuning bandwidth, spectrally resolved values Dλ,exp.(λ) are obtained. This is shown in Fig. 5 for various increments. While the measurements within their error bars consistently agree with the reference measurement, the increasing error bars for higher spectral resolutions limit the significance of the measurement. In this area, interferometric methods are more suitable.
The advantages of dispersion measurement with the TCFL, however, are based on automated measurements in a stable fiber-integrated design without the need for any allignment. This makes it particularly interesting for industrial applications in quality management, as well as for fiber laser applications.
Funded by: BMBF, DFG