- Home
- Research
- Fiber Photonics
- Research results
- Guiding Light in Anti-Resonant Hollow-core Fibers
Guiding Light in Anti-Resonant Hollow-core Fibers
12.04.2018
In this contribution, we will describe an analytical model for the effective index of anti-resonant fibers. Since in all practically-relevant cases the core diameter is large in comparison to the wavelength, the problem can be traced back to the reflection of the guided light under grazing incidence. This enables the derivation of analytical approximation formulas for the real and imaginary part of the effective index.
By: Matthias Zeisberger // Markus A. Schmidt
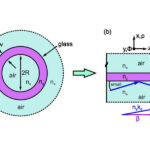
Microstructured hollow-core fibers are a current research topic that promises interesting applications, for example in surgery, for lasers in the mid-IR range, tunable UV sources, non-linear optical effects, the generation of high-power laser pulses, photothermal trace analysis in gases, microparticle detection, and pulse compression. Since the core medium in hollow-core fibers generally has a lower refractive index than the media surrounding the core, wave guiding is not based on total reflection and is, therefore, lossy. These losses can be reduced if the core diameter (2 R) is large compared to the wavelength (λ). The hollow-core fibers currently being used typically have a core diameter of several 10 μm. In this case, the light guiding of the lowest modes corresponds to a reflection at a very shallow angle of incidence (θ = π/2 – ψ, ψ ≪ 1), which leads to a very high reflectivity and thus low losses. A further improvement can be achieved by microstructuring the medium. A simple configuration that is well suited for understanding the basic effects is a fiber in the shape of a thin hollow cylinder (with a wall thickness w of several 100 nm), which consists, for example, of fused silica (refractive index ng ≈ 1.45) and surrounds an air or gas-filled core (radius R, refractive index na ≈ 1.0). The outer medium is the same as in the core (see Fig. 1).
Analytical Formula
The given ratios (λ≪R) make it possible to find an analytical approximation formula for the complex effective index, similar to our previous investigations of the metamaterial fiber using an interference method (interference parameter σ=λ/2 π R):
neff = na – a σ2 – b σ3 + i d σ4,
wherein the parameters a, b, and d are real. The last term represents the losses which, in contrast to the metamaterial fiber, show a 1/R4 dependence. The parameters b and d describe the resonances of the fiber.
Findings
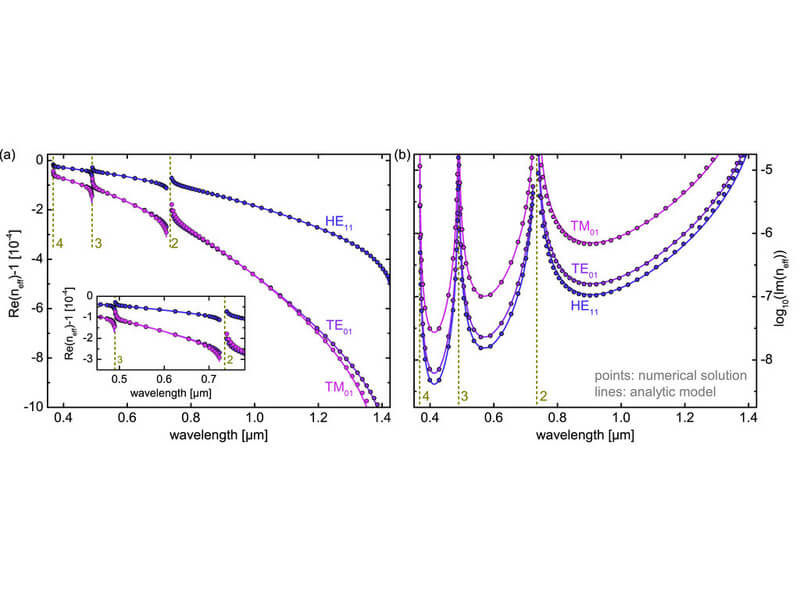
The resulting analytical formula was compared with numerical simulations and shows a very good agreement for the different types of modes, as well as a wide range of core radii and wavelengths (see Fig. 2). Thus, the analytical formula is well suited to determine the basic parameters when designing anti-resonant fibers, since the dependence of properties on geometry and material parameters is clearly evident and calculations with parameter variations can be carried out faster than on the basis of numerical simulations.
An interesting aspect is the group velocity dispersion (GVD), which plays an important role in nonlinear effects such as supercontinuum generation. In order to optimize such processes, it is necessary to know the dependence of the GVD on wavelength, geometry, and material parameters. These investigations are considerably simplified by the analytical formula. It becomes evident that the anti-resonant fiber offers more degrees of freedom for influencing the GVD. In particular, the geometry can be selected in such a way that the material dispersion of the core material can be compensated for the desired working wavelength by the effects of the anti-resonant fiber.
Funded by: DFG, TMWWDG